Archives of Pharmacy and Pharmaceutical Sciences

Research Article

You Are Here:

A Further Example Showing Efficiency of a Modeling Method Based on the Theory of Dynamic Systems in Pharmacokinetics

Maria Durisova*

Department of Pharmacology of Inflammation, Institute of Experimental Pharmacology and Toxicology, Slovak Academy of Sciences, Dubravska Street, 841 04 Bratislava, Slovak Republic

*Address for Correspondence: Mária Ďurišová, Slovak Academy of Sciences, Institute of Experimental Pharmacology and Toxicology, Bratislava, Slovak Republic, Tel: 00421254775928; Email: maria.durisova@savba.sk

Dates: Submitted: 21 December 2016; Approved: 23 January 2017; Published: 25 January 2017

How to cite this article: Durisova M. A Further Example Showing Efficiency of a Modeling Method Based on the Theory of Dynamic Systems in Pharmacokinetics. Arch Pharm Pharm Sci. 2017; 1: 007-012. DOI: 10.29328/journal.apps.1001002

Copyright License: © 2017 Durisova M. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Keywords: Dynamic system; Mathematical model; Transfer function.

Abbreviations: ADME: Absorption Distribution Metabolism Excretion; CTDB: Clinical Trials DataBase

ABSTRACT

Aims: To present a further example showing an efficiency of a modeling method based on the theory of dynamic systems in pharmacokinetics.

Study design:The goals of the current study were twofold: to present (1) a further example showing efficiency of a modeling method based on the theory of dynamic systems in pharmacokinetics, an to perform (2) a next step in tutoring the use of computational and modeling tools from the theory of dynamic systems in pharmacokinetics.

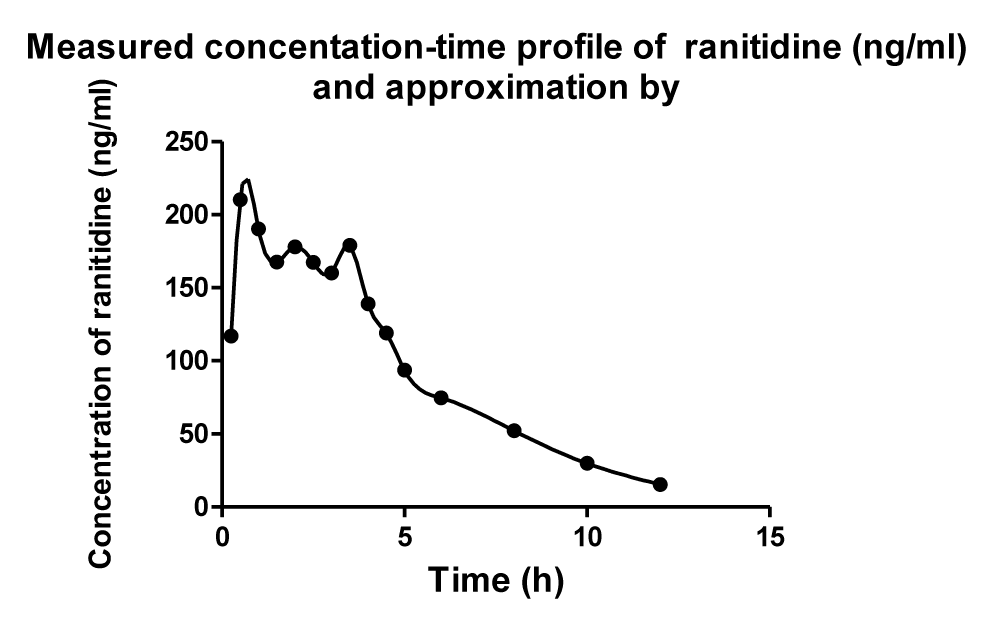
The data available in the study by Plusquellec et al. published in the October Issue of the Journal Medical Engineering & Physics were used to exemplify the method considered here. For modeling purpose an advanced mathematical modeling method was employed. Modeling was performed using the computer program named CTDB described in the study by Dedík et al. published in September 2007 issue of the Journal Diabetes Research and Clinical Practice.

Main outcome: Modeling results revealed that computational and modeling tools from the theory of dynamic systems can be successfully used in the development of a mathematical model of such a complicated process as is a multiple sites discontinuous gastrointestinal absorption.

INTRODUCTION

Ranitidine is a histamine H2-receptor antagonist with a potent and long-acting antisecretory effect in humans that significantly improves the quality of gastric ulcer healing and histological scores of gastric mucosa in patients with gastric ulcers. In addition, ranitidine was successfully utilized in the treatment of active duodenal ulcers and gastric hypersecretory, where the inhibitory effect of ranitidine on the gastric secretion was much longer than that of cimetidine. Ranitidine is a widely used drug and is known to be well tolerated by patients. Ranitidine is commonly used in treatment of peptic ulcer disease, gastroesophageal reflux disease, and Zollinger-Ellison syndrome it is possibly more effective than cimetidine [1-10].

The goals of the current study were twofold: 1) to present a further example showing efficiency of a modeling method based on the theory of dynamic systems in pharmacokinetics; 2) to exemplify the modeling method considered here, using the data available in the study by Plusquellec et al. published in October 1999 Issue of the Journal Medical Engineering & Physics.

METHODS

The data available in the study cited above employed. For modeling purposes the computer program named CTGB described in the study by Dedík et al. published in September 2007 issue of the Journal Diabetes Research and Clinical Practice was employed.

Throughout the current study, the lower case letter “S” was used for the complex Laplace variable [10-24]. The development of a mathematical model of the pharmacokinetic behavior of ranitidine [1-9] was performed in the following successive steps:

(1) The definition of an ADME-related dynamic pharmacokinetic system [25] denoted by H, using: the Laplace transform of the mathematically described serum concentration-time profile of ranitidine, denoted by C(s), and the Laplace transform of the mathematically described oral administration of ranitidine [7], denoted by I(s). In the definition of the ADME-related dynamic pharmacokinetic the profile C(s) and the profile I(s) was used as the output and input, respectively, of the ADME-related dynamic pharmacokinetic system H [10-24].

(2) The introduction of the following simplifying assumptions: a) initial conditions of the ADME-related dynamic pharmacokinetic system were zero; b) all processes mathematically described by the ADME-related dynamic pharmacokinetic system were linear and time invariant [10-24]; c) concentrations of ranitidine were the same throughout all subsystems of the ADME-related dynamic pharmacokinetic system, (where each subsystem was an integral part of the ADME-related dynamic pharmacokinetic system).

(3) The static and dynamic properties of the pharmacokinetic behavior of orally administered ranitidine [25-27] were described with the ADME-related dynamic pharmacokinetic system;

(4) The transfer function, denoted by H(s), of the ADME-related dynamic pharmacokinetic system was derived, using the profiles C(s) and I(s), see Eq. (1).

H(s)= C(s) I(s) .(1) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbdfwBIjxAHbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8qrps0lbbf9q8WrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciaacaGaaeqabaWaaqaafaaakeaacaWGibGaaiikaiaadohacaGGPaGaeyypa0ZaaSaaaeaacaWGdbGaaiikaiaadohacaGGPaaabaGaamysaiaacIcacaWGZbGaaiykaaaacaGGUaGaaiikaiaaigdacaGGPaaaaa@45CB@

(5) The ADME-related dynamic pharmacokinetic system was described with the transfer function H(s) in the complex domain.

In the following text, the ADME-related dynamic pharmacokinetic system was simply called the dynamic system

(6) The mathematical model of the dynamic system was developed using the computer program named CTDB [15] and the transfer function model HM(s) described by the following equation:

H M (s)=G a 0 + a 1 s+...+ a n s n 1+ b 1 s+...+ b m s m .(2) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbdfwBIjxAHbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8qrps0lbbf9q8WrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciaacaGaaeqabaWaaqaafaaakeaacaWGibWaaSbaaSqaaiaad2eaaeqaaOGaaiikaiaadohacaGGPaGaeyypa0Jaam4ramaalaaabaGaamyyamaaBaaaleaacaaIWaaabeaakiabgUcaRiaadggadaWgaaWcbaGaaGymaaqabaGccaWGZbGaey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSIaamyyamaaBaaaleaacaWGUbaabeaakiaadohadaahaaWcbeqaaiaad6gaaaaakeaacaaIXaGaey4kaSIaamOyamaaBaaaleaacaaIXaaabeaakiaadohacqGHRaWkcaGGUaGaaiOlaiaac6cacqGHRaWkcaWGIbWaaSbaaSqaaiaad2gaaeqaaOGaam4CamaaCaaaleqabaGaamyBaaaaaaGccaGGUaGaaiikaiaaikdacaGGPaaaaa@5B71@

On the right-hand-side of Eq. (2) is the Padé approximant [28,29] of the mathematical model of the transfer function HM(s), G is an estimator of a model parameter called a gain of a dynamic system, a 1 ,⋯ a n , b 1 ,⋯ b m MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbdfwBIjxAHbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8qrps0lbbf9q8WrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciaacaGaaeqabaWaaqaafaaakeaacaWGHbWaaSbaaSqaaiaaigdaaeqaaOGaaiilaiabl+UimjaadggadaWgaaWcbaGaamOBaaqabaGccaGGSaGaamOyamaaBaaaleaacaaIXaaabeaakiaacYcacqWIVlctcaWGIbWaaSbaaSqaaiaad2gaaeqaaaaa@4648@ are additional model parameters, and n is the highest degree of the nominator polynomial, and m is the highest degree of the denominator polynomial, n is the highest degree of the nominator polynomial, and n < m (see Eq. (2)) [9-24].

(7) The transfer function H(s) was converted into equivalent frequency response function, denoted by F(iω) [29].

Table 1: Parameters of the fourth-order model of the dynamic system describing the dynamic pharmacokinetic behavior of orally administered ranitidine [1].
Model parameters Estimates of
model parameters		 (95% CI)
G (h.l-1) 0.0097 0.006 to 0.012
a0 (-) 0.923 0.825 to 1.024
a1 (min) 69.15 45.12 to 72.38
b1 (min) 421.88 391.73 to 462.02
b2 (min2) 6043.61 7028.59 to 6059.33
b3 (min3) 3478275.74 3478271.05 to 3678280.33
b4 (min4) 5825685.25 29456822.06 to 6234685.25
Table 2: Model-based estimates of pharmacokinetic variables of orally administered ranitidine [1].
Primary pharmacokinetic variables Estimates of primary
pharmacokinetic
variables
The half-time of
Ranitidine t½ (hod)		 1.5±0.4*
Clearance of ranitidine (ml/min) 103.1±15.3
Renal clearance of ranitidine
(ml/min) 		74.1±5.1
Body clearance of ranitidine (ml/min) 218±8.1
Elimination half-life of ranitidine (hr) 51.6±5.4
Distribution volume of ranitidine (l) 681±9.5
AUCo®¥ (ng.h/ml) 26.95
*standard deviation

Figure 1: Patient 24, varying maximum activity in visual comparison of I-131 scintigram (1a) with the Tc-99m-O4- scintigram (1b). Grid image in Figure 1a highlighted by the use of a high-energy collimator.

(8) The non-iterative method described in the study published previously [29] was used to develop a mathematical model of the frequency response function FM(iωj) and to determine point estimates of parameters of the model of the frequency response function FM(iωj) in the complex domain. The model of the frequency response function FM(iωj) used in the current study is described by the following equation:

F M (i ω j )=G a 0 + a 1 i ω j +...+ a n (iω) n 1+ b 1 i ω j +...+ b m (i ω j ) m .(3) MathType@MTEF@5@5@+=feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbdfwBIjxAHbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8qrps0lbbf9q8WrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciaacaGaaeqabaWaaqaafaaakeaacaWGgbWaaSbaaSqaaiaad2eaaeqaaOGaaiikaiaadMgacqaHjpWDdaWgaaWcbaGaamOAaaqabaGccaGGPaGaeyypa0Jaam4ramaalaaabaGaamyyamaaBaaaleaacaaIWaaabeaakiabgUcaRiaadggadaWgaaWcbaGaaGymaaqabaGccaWGPbGaeqyYdC3aaSbaaSqaaiaadQgaaeqaaOGaey4kaSIaaiOlaiaac6cacaGGUaGaey4kaSIaamyyamaaBaaaleaacaWGUbaabeaakiaacIcacaWGPbGaeqyYdCNaaiykamaaCaaaleqabaGaamOBaaaaaOqaaiaaigdacqGHRaWkcaWGIbWaaSbaaSqaaiaaigdaaeqaaOGaamyAaiabeM8a3naaBaaaleaacaWGQbaabeaakiabgUcaRiaac6cacaGGUaGaaiOlaiabgUcaRiaadkgadaWgaaWcbaGaamyBaaqabaGccaGGOaGaamyAaiabeM8a3naaBaaaleaacaWGQbaabeaakiaacMcadaahaaWcbeqaaiaad2gaaaaaaOGaaiOlaiaacIcacaaIZaGaaiykaaaa@6B85@

Analogously as in Eq. (2), n is the highest degree of the numerator polynomial of the model of the frequency response function FM(iωj), m is the highest degree of the denominator polynomial of the mathematical model of the frequency response function FM(iωj), n ≤ m, i is the imaginary unit, and ω is the angular frequency in Eq. (3).

The Akaike information criterion, modified for the use in the complex domain [9,30] was employed to select the best mathematical model of the frequency response function FM(iωj) and to determine point estimates of the parameters of the best mathematical model of the frequency response function FM(ij).

Finally, the Monte-Carlo and the Gauss-Newton method [31,32] were used to refine the mathematical model of the frequency response function FM(iωj) and to determine 95 % confidence intervals of the parameters of the best mathematical model of the frequency response function FM(iωj) in the time domain.

After the development of the best mathematical model FM(iωj) of the dynamic system investigated, the following primary pharmacokinetic variables of ranitidine were determined: the elimination half-time of ranitidine, denoted by t½, the area under the serum concentration-time profile of ranitidine from time zero to infinity, denoted by, AUCο-∞, and total body clearance of ranitidine, denoted by CI.

The mathematical model of the transfer function HM(s) and the mathematical model of the frequency response function FM(iωj) are implemented in the computer program CTDB [15]. A demo version of the computer program CTDB is available at the following web site of the author: http://www.uef.sav.sk/advanced.htm

REFERENCES

  1. Dammann HG, Müller P, Kather H, Simon B. The new histamine H2-receptor antagonist ranitidine. Duration of action. Res Exp Med (Berl). 1981; 178: 151-154. Ref.: https://goo.gl/47Zy9Y
  2. Dawson J, Richards DA, Stables R, Dixon GT, Cockel R. Ranitidine --pharmacology and clinical use. J Clin Hosp Pharm Ther. 1983; 8: 1-13. Ref.: https://goo.gl/bkzNwF
  3. Eckardt VF, Cordes I, Janish HD, Wiemann H. Daytime acid secretion after a single dose of ranitidine and cimetidine--a double blind crossover study. Eur J Clin Pharmacol. 1984; 26: 177-182. Ref.: https://goo.gl/9HoAnV
  4. Brittain RT, Jack D. Histamine H2-antagonists--past, present and future. J Clin Gastroenterol. 1983, 5: 71-79. Ref.: https://goo.gl/EXuI0O
  5. Gaginella TS, Bauman JH. Ranitidine hydrochloride. Drug Intell Clin Pharm 1983; 17: 873-885. Ref.: https://goo.gl/ptOQfC
  6. Merki HS, Witzel L, Walt RP, Neumann J, Scheurle E, et al. Comparison of ranitidine 300 mg twice daily, 300 mg at night and placebo on 24-hour intragastric acidity of duodenal ulcer patients. Aliment. Pharmacol Ther. 1987; 1: 217-223. Ref.: https://goo.gl/bEZhOc
  7. Plusquellec Y, Efthymiopoulos C, Duthil P, Houin G. A pharmacokinetic model for multiple sites discontinuous gastrointestinal absorption. Med Eng Phys. 1999; 21: 525-532. Ref.: https://goo.gl/BkULJt
  8. Reid SR, Bayliff CD. The comparative efficacy of cimetidine and ranitidine in controlling gastric pH in critically ill patients. Canad Anaesth. 1986; 33: 287-293. Ref.: https://goo.gl/Wcm42c
  9. Higuchi K, Watanabe T, Tominaga K, Shiba M, Nakagawa K, et al. Effects of ranitidine on quality of gastric ulcer healing compared with famotidine: a randomized, controlled, multicenter trial. Int J Clin Pharmacol Res. 2005; 25: 187-194. Ref.: https://goo.gl/i6D1S1
  10. Chrenova J, Durisova M, Mirciou C, Dedik L. Effect of gastric emptying and entero-hepatic circulation on bioequivalence assessment of. Methods Find Exp Clin Pharmacol. 2010; 32: 413-419. Ref.: https://goo.gl/OanMbq
  11. van Rossum JM, de Bie JE, van Lingen G, Teeuwen HW. Pharmacokinetics from a dynamical systems point of view. J Pharmacokinet Biopharm. 1989; 17: 365-392. Ref.: https://goo.gl/VAVsFe
  12. Dedík L, Ďurišová M. CXT-MAIN: a software package for the determination of the analytical form of the pharmacokinetic system weighting function. Comput Methods Programs Biomed. 51: 183-192. Ref.: https://goo.gl/iAvtNQ
  13. Dedík L, Ďurišová M. Frequency response method in pharmacokinetics. J Pharmacokin Biopharm. 1994; 22: 237-307. Ref.: https://goo.gl/flpLxF
  14. Ďurišová M, Dedík L. Modeling in frequency domain used for assessment of in vivo dissolution profile. Pharm Res. 1997; 14: 860-864. Ref.: https://goo.gl/p6uWjQ
  15. Ďurišová M, Dedík L. A system-approach method for the adjustment of time-varying continuous drug infusion in individual patients: A simulation study. J Pharmacokinet Pharmacodyn. 2002; 29: 427-444. Ref.: https://goo.gl/1XtK6n
  16. Ďurišová M, Dedík L. New mathematical methods in pharmacokinetic modeling. Basic Clin Pharmacol Toxicol. 2005; 96: 335-342. Ref.: https://goo.gl/UNFNoG
  17. Yates JW. Structural identifiability of physiologically based pharmacokinetic models. J Pharmacokinet Pharmacodyn. 2006; 33: 421-439. Ref.: https://goo.gl/qf3HvZ
  18. Ďurišová M, Dedík L, Kristová V, Vojtko R. Mathematical model indicates nonlinearity of noradrenaline effect on rat renal artery. Physiol Res. 2008; 57: 785-788. Ref.: https://goo.gl/UW4Ees
  19. Ďurišová M. Physiologically based structure of mean residence time. Scientific World Journal. 2012. Ref.: https://goo.gl/DjpTgU 
  20. Ďurišová M. A physiological view of mean residence times. Gen Physiol Biophys. 2014; 33: 75-80. Ref.: https://goo.gl/SFZu6S
  21. Ďurišová M. Mathematical model of pharmacokinetic behavior of orally administered prednisolone in healthy volunteers. J Pharmaceut & Pharmacol. 2014; 2:  1-5.
  22. Ďurišová M. Further worked out examples that illustrated the successful use of an advanced mathematical modeling method based on the theory of dynamic systems in pharmacokinetics. Int J Res Sci Res. 2015; 6: 4873-4879. Ref.: https://goo.gl/eB8xLo 
  23. Ďurišová M. Mathematical model of pharmacokinetic behavior of warfarin. Adv Pharm Clin Trials. 2016; 1: 1-7. Ref.: https://goo.gl/1Zd7zi
  24. Ďurišová M. Computational analysis of pharmacokinetic behavior of ampicillin. J Appl Bioanal. 2016; 2: 84-89. Ref.: https://goo.gl/9uhDJ6
  25. Levitt DG. PK Quest: a general physiologically based pharmacokinetic model. Introduction and application to propranolol. BMC Clin Pharmacol. 2002; 15: 2-5. Ref.: https://goo.gl/2UCayb
  26. Howell BA, Yang Y, Kumar R, Woodhead JL, Harill AH, et al. In vitro to in vivo extrapolation and species response comparisons for drug-indused liver injury (DILI) using DILsymTM: a mechanistic model of DILI. J Pharmacokinet Pharmacodyn. 2012; 39: 527-541. Ref.: https://goo.gl/LveVQu
  27. Dedík L, Ďurišová M, Penesová A, Miklovičová D, Tvrdoňová M. Estimation of influence of gastric emptying on shape of glucose concentration-time profile measured in oral glucose tolerance test. Diabetes Research and Clinical Practice. 2007; 77: 377-384. Ref.: https://goo.gl/0koO9F
  28. Ďurišová M. Physiologically based structure of mean residence time. The Sci World Journal. 2012. Ref.: https://goo.gl/xPqy08
  29. Ďurišová M. A physiological view of mean residence times. Gen Physiol Biophys. 2014; 33: 75-80. Ref.: https://goo.gl/44tImL
  30. Weiss M, Pang KS. Dynamics of drug distribution. I. Role of the second and third curve moments. J Pharmacokinet Biopharm. 1992; 20: 253-278. Ref.: https://goo.gl/wiYtGU
  31. Verotta D. Concepts, properties, and applications of linear systems to describe distribution, identify input, and control endogenous substances and drugs in biological systems. Crit Rev Biomed Eng. 1996; 24: 73-139. Ref.: https://goo.gl/6lGcmI
  32. Xiao H, Song H, Yang Q, Cai H, Qi R,et al. A prodrug strategy to deliver cisplatin (IV) and paclitaxel in nanomicelles to improve efficacy and tolerance. Biomaterials. 2012;  33: 6507-6519. Ref.: https://goo.gl/UthCGZ
  33. Beckermann B, Kaliaguine V. The diagonal of the Padé table and the approximation of the Weyl function of second-order difference operators. Constr Approx. 1997; 13: 481-510. Ref.: https://goo.gl/AgA5a2
  34. Levy EC. Complex curve fitting. IRE Trans Automat Contr. 1959; 4: 37-43. Ref.: https://goo.gl/5g3G6d 
  35. Akaike H. A new look at the statistical model identification. IEEE Trans Automat Contr. 1974; 19: 716-723. Ref.: https://goo.gl/KM0Sbt 
  36. Lampariello F, Sciandrone M. Use of the minimum-norm search direction in a nonmonotone version of the Gauss-Newton method. J Optim Ther Appl. 2003; 119: 65-82. Ref.: https://goo.gl/JwG01Y
  37. Boyle P. Options: A Monte Carlo approach. J Fin Econom. 1977; 4: 323-338. Ref.: https://goo.gl/g8gMCC
  38. Varvel JR, Donoho DL, Shafer SL. Measuring of the predictive performance of computer controlled infusion pumps. J Pharmacokin Biopharm. 1992; 20: 63-84. Ref.: https://goo.gl/vsRmMu
  39. Siegel RA. Pharmacokinetic transfer functions and generalized clearances. J Pharmacokin Biopharm. 1986; 14: 511-521. Ref.: https://goo.gl/aRrc7I
  40. Segre G. The sojourn time and its prospective use in pharmacology.J Pharmacokin Bio- pharm. 1988; 16: 657-666. https://goo.gl/7yZs2V
  41. Yates JW. Structural identifiability of physiologically based pharmacokinetic models. J Pharmacokinet Pharmacodyn. 2006; 33: 421-439. Ref.: https://goo.gl/VPEqJ0
  42. Rescigno A. Compartmental analysis and its manifold applications to pharmacokinetics. AAPS J. 2010; 12: 61-72. Ref.: https://goo.gl/qJ6h5r
  43. Gillespie WR, Veng-Pedersen P, Berg MJ, Schkottelius DD. Linear systems approach to the analysis of an induced drug removal process. Phenobarbital removal by oral activated charcoal. J Pharmacokin Biopharm. 1986; 14: 19-28. Ref.: https://goo.gl/vL520R
Journal Home About Journal Editors Archive Submit Manuscript