Application of the Pyphagor’s Theorem for Correction of Ki and Ka constants of enzyme inhibition and activation

VI Krupyanko1* and PV Krupyanko2
1GK Skryabin Institute of Biochemistry and Physiology of Microorganism, Russian Academy of Sciences, 142290 Pushchino, Moscow Region, Prospect Nauki 5, Russia
2Center for Information Technologies on Transport LLC, 142060, Moskow, Domodedovo, MK-Region Barybino, str. Yuzhnaya 17, Russia
*Address for Correspondence: Vladimir I Krupyanko, GK Skryabin Institute of Biochemistry and Physiology of Microorganism, Russian Academy of Sciences, Town Pushchino, Prospekt Nauki 5, Moscow Region, Russia, 142290, Tel: (495) 625-74-48; Fax: 956-33-70; Email: [email protected]
Dates: Submitted: 19 September 2018; Approved: 29 October 2018; Published: 30 October 2018
How to cite this article: Krupyanko VI, Krupyanko PV. Application of the Pyphagor’s Theorem for Correction of Ki and Ka constants of enzyme inhibition and activation. Arch Pharm Pharma Sci. 2018; 2: 060-068. DOI: 10.29328/journal.apps.1001011
Copyright License: © 2018 Krupyanko VI, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Quadratic forms of equations for correction of Ki and Ka constants

Abstract
The analysis of dependence of the length projection of Li vectors of biparametrical inhibited and activated (La) enzymatic reactions from the length projection of vectors of monoparametrical inhibited and activated enzymatic reactions on the basic σ0 plane in three-dimensional coordinate system, allows to deduct the quadratic forms of equations for the correction of the constants of inhibition (ki) and activation (Ka) of enzymes. Examples of correction of constants are given.
Introduction
The study inhibition of enzymes helps to synthesize the drugs from poisoning of living organisms.
In previous articles [1-9], devoted to construction of a vector method representation of enzymatic reactions in the three-dimensional K’m V’ I coordinate system the properties of L vectors of enzymatic reactions was analyzed, from which the parametriacal classification of the types of enzymatic reactions and the equations for calculation of initial activated (va) and inhibited (vi) reaction rates was deduced. In articles [2-9] the equations of traditional form (t.f.) for calculation of the constants of activation (Ka) and absent in practice the equations of nontrivial types of biparametrical constants of inhibition (ki) of enzymes (Table 1), was deduced [5].
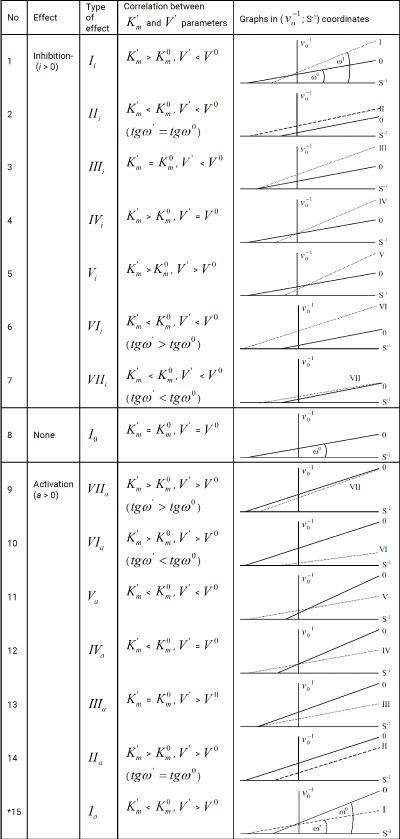
Table 1: Equations for calculation of Ki and Ka constants (in traditional form). *The symbol of a graph in Figure. 1-15 corresponds to the type of reaction under study. For example: the line (0) characterizes the position of initial (nonactivated) enzymatic reaction, line I – the position of a graph representing the Ia type of activated enzymatic
reaction etc.
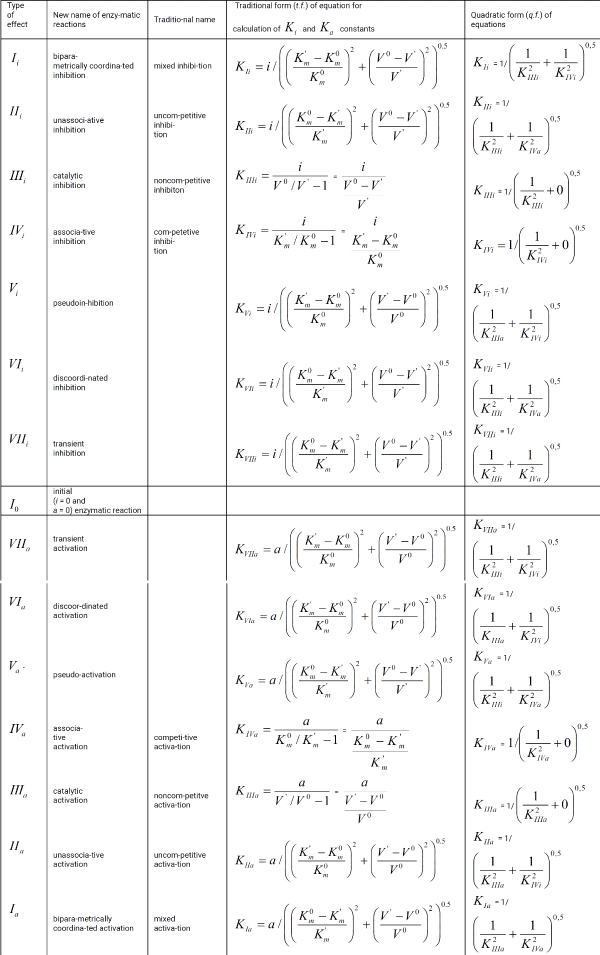
Table 1 continued.:
This work is devoted to deduction of quadratic form (q.f.) of the equations for correction of biparametrical constants of inhibition Ki and activation Ka of enzymes (Table 1, q.f.), opening additional ability in the analysis of enzyme action what help of these equations.
The examples of comparative using traditional and quadratic form of equations for correction of Ki and Ka constants of enzyme inhibition and activation are given.
Deduction of traditional form of equations
From Figures 1 and 2 it easy to see, that (
) length of (LIi) projection of LIi vector of biparametrically coordinated, Ii type (or mixed type [10-12] of enzyme inhibition) on Pi semiaxis will be determined by difference: (i-0) parameters, The basic σ0 plane (Figure 2), actually is orthogonal projection of three-dimensional L vectors of (Figure 1), i.e. the scalar magnitudes (orthogonal between them self) LIIIi and LIVi projections of monoparametrical LIIIi and LIVi vectors of IIIi and IVi type of enzyme inhibition, (which also are the coordinate of these vectors) but in the same time they taking adjacent place relative to orthogonal LIi projection of LIi vector (Figure 2), determined by equation:
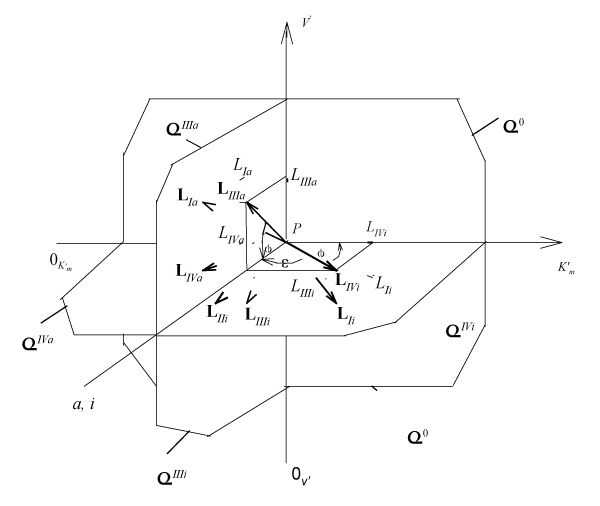
Figure 1: Three-dimensional (packed)
system of rectangular coordinates with coincident Pi and Pa semiaxes of molar concentrations of inhibitor i and activator a. The symbols of kinetic parameters:
three-dimensional vectors: LIi, LIVi… LIa, LIVa, LIi, LIVi…, and their projections LIi, LIVi… LIa, LIVa on the basic σ0 plane as well as the symbols of projections of directing planes σIVi, σIIIi, σIVα, σIIIα on the
and
coordinate semiaxes the same as in the text.
It is analogous for length of adjacent projections of LIIi, LVi … and LIa, LIIa, LVa … for all other LIIi, LVi … , LIa, LIIa, LVa … three-dimensional vectors of biparametrical reactions (Figure 2).
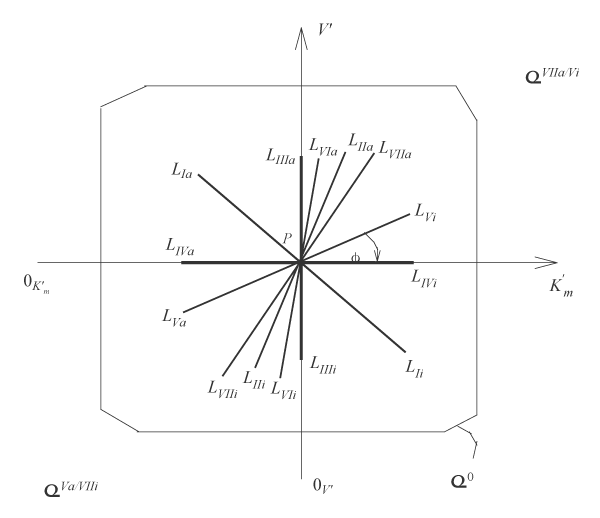
Figure 2: Two-dimensional (scalar)
coordinate system. The symbols of kinetic parameters:
the projections LIi, LIVi… LIa, LIVa of three-dimensional vectors: LIi, LIVi… LIa, LIVa on the basic 0 plane and symbols of
and
coordinate semiaxes the same as in Figure 1 and in the text.
Having expressed from Eqn. (2)
the lIIIi length of dimensionless of LIIIi projection of LIIIi vector on P0V’ semiaxis of K’m V’ I coordinate (Figure 1) and from Eqn. (3)
the lIVi length of the second adjacent dimensionless of LIVi vector projection on PK’m semiaxis and substituted them in Eqn. (4):
we shall obtain traditional form (t.f.) of equation for calculation of the
constant of biparametrically coordinated, Ii type, inhibition of enzymes, taking in to consideration the lIi length of orthogonal projection of LIi vector on basic σ0 plane of figure 1:
Similarly for deduction of all biparametrical equations of table 1 [5,7,8].
Deduction of quadratic form of equations
From analysis of equations (1 – 4) one can easily see that substitution in Eqn. (4) of the dimensionless coordinates of the lengths of
and
vector projections is equal to substitution in this equation of the
and
parameters
then it is not difficult to become the quadratic forms of equations for correction of Ki and Ka constants of biparametrical types of inhibition and activation of enzymes (Table 1).
For example, such as:
this substitution will leads to equation:
or, in quadratic form:
convenient for correction of constant inhibition of enzymes (Eqn. 1, q.f., Table 1).
It is analogous for all the other equations of biparametrical types of inhibition (Eqns. 2, 5 – 7), and activation (Eqns. 9 – 11 and 14, 15) of enzymes, (Table 1, q.f.) taking into account, orthogonal projections of tree-dimensional L vectors on the basic σ0 plane of (Figure 1) by data analysis of correspond position two-dimensional scalar L projections of L vectors on these vectors in K’mV’ coordinate system (Figure 2). For example, the orthogonal projection length of LIa vector of,
type, activation will be determined by analogous common equation (1, text) of enzyme activation that is located in the σ0 plane of scalar K’mV’ coordinate system (Figure 2, in IInd quadrant) and edged by two
and
lengths of edged projection of this vector on the PV’ and P0Km semiaxes (lIa =
),
a) in equation of lIIi length projection – by two lIVa and lIIIi lengths of edged vector projections (
);
b) in equation of lVi length projection – lIVi and lIIIa lengths of edged vector projections (
) and so on.
Examples of constants correction
Example 1: Calculation of
constant inhibition.
The inhibitory effect of Tungstic acid anions WO
(0.510-4 M)
on the initial rate of pNPP cleavage by calf alkaline phosphatase figure 3 shows that the presence 0.510-4 M of these anions in the enzyme-substrate system makes the binding of the enzyme to the substrate cleaved (
= 4.4510-5 M,
= 6.5610-5 M) difficult and leads to a decrease in the maximum reaction rate (V0 = 2.56, V’ = 1.74 µmol/(min per µg protein). This meets all the features (
) of the biparametrically coordinated, Ii type, of enzyme inhibition (Table 1, line 1). Hence, to calculate the KIj constant of this enzyme inhibition it is necessary to use Eqn. (5, text), or (Eqn. 1, t.f., Table 1).
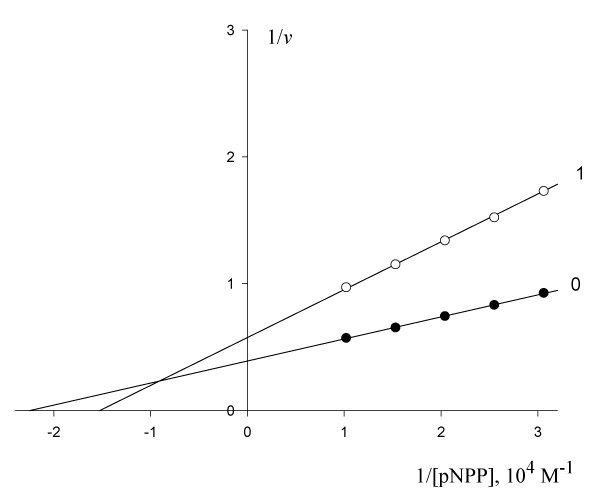
Figure 3: Inhibitory effect of anions WO on the initial rate
, µumol/(min per µg protein) of pNPP cleavage by calf alkaline phosphatase.
Note: line 1 – the concentration of WO
is 0.510-4 M; line (0) – the inhibitor is absent.
Substitution in this equation of the parameters and
obtained by data analysis of (Figure 3) allows the calculation of this constant of enzyme inhibition:
Substitution of these parameters rewritten to forms with (
= 1.062 10-4 M,
= 1.055 10-4 M) in (Eqn. 1, q.f., Table 1)
result in to the same value of the constant of enzyme inhibition:
From Eqns. (10 – 12) it follows that dimension of KIi constants in all cases, are the molar concentration of inhibitor:
Сorrection. Determine the value of the KIVi constant of this experiment (Figue 3) by values of KIi and KIIIi constants.
From equation (11), rewritten to the form,
it follows that:
Substitution the necessary parameters from (Eqn. 14) to (Eqn. 15), we find that:
which is in good agreement with the experimental value of this constant (Eqn. 10).
Example 2: Calculation of KVi constant inhibition.
The inhibitory effect of Pyrrolidine dithiocarbonic acid (PDTA) on the initial rate of pNPP cleavage by canine alkaline phosphatase shows that in the presence of 1·10-3 М PDTA the parameters
= 4.69·10-5 М and
= 2.921 µmol/(min per µg protein) change as follows:
11.26·10-5 М and
= 3.616 µmol/(min per µg protein) (Figure 4). This corresponds to the, Vi type, of enzyme pseudoinhibition (
>
,
>
,
> 0) (Table 1, line 5) and Eqn. (5, t.f.) is applicable for calculation of the KVi constant of enzyme inhibition. Substitution all necessary parameters in this equation allow calculation of this constant of enzyme inhibition:
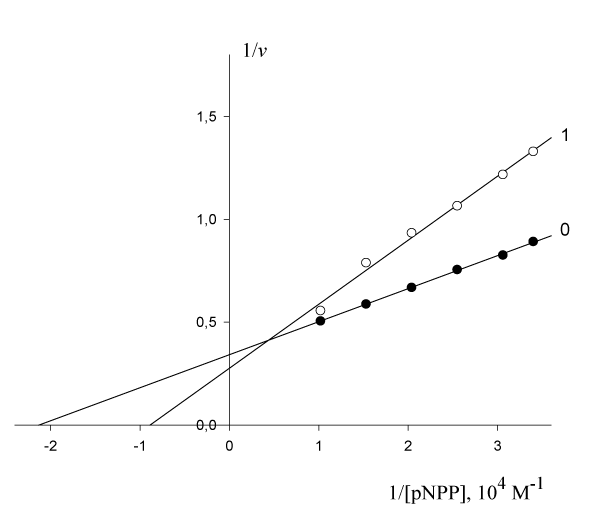
Figure 4: Inhibitory effect of PDTA on the initial rate
, µumol/(min per µg protein) of pNPP cleavage by canine alkaline phosphatase.
Note: line 1 – the concentration of PDTA is 1·10-3 M; line (0) – the inhibitor is absent.
Substitution all necessary parameters from of recalculated parameters of (Figure 4) to (Eqn. 5, Table 1, q.f.) – result in to value of KVi constant inhibition:
rewritten to the forms (KIVi = 0.714 10-3 М and KIIIa = 4.203 10-3 М)
from which it follows that
Example 3: Calculation of KVa constant activation.
The results of study presented in figure 5 show that: the parameters of initial non-activated reaction of pNPP cleavage by alkaline phosphatase
= 5.45·10-5 М, V0 = 9.363 µmol/(min µg protein) in the presence of 0.001 M of activator change as follows:
= 3.47·10-5 М, V’ = 8.803 µmol/(min µg protein), which satisfies all the features of type Va of enzyme pseudoactivation (line 11, Table 1).
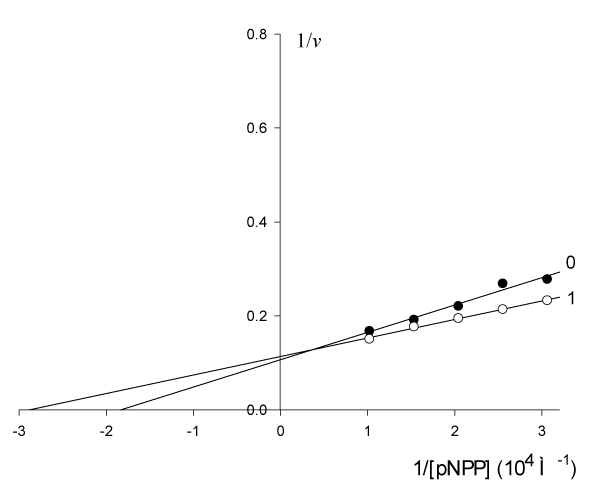
Figure 5: Activating effect of Guo on the initial rate
, µmol/(min per µg protein) of
pNPP cleavage by canine alkaline phosphatase.
Note: line 1 – the concentration of Guo is 1·10-3 M; line (0) – the activator is
absent.
Substitution of the experimental parameters of (Figure 5, in Eqn. 11, t.f., Table 1) gives the following value of KVa constant:
or according Eq. 11, Table 1)
Example 4: Calculate the value of KIIIi constant of experiment (Figure 3), by value of KIi and KIVi constants.
From equation (1, Table 1, t.f.), rewritten to the form (22)
it follows that:
Having substituted all necessary parameters from (Eqn. 22) into (Eqn. 23), the next value of this constant is received:
Example 5: Calculate the value of KIIIa constant of experiment (Figure 5), by value of KVa and KIVi constants.
From equation (11, Table 1, t.f.), rewritten to the form (22)
it follows that:
It is no desirable to put KVa = 1.74∙10-3 М from (Eqn. 20) in (Eqn. 25), because calculation leads to KIIIa = 14.43 10-3M (instead 15.66 10-3 M), such as the first constant is not in Pythagorean´s «bundle» (Egn. 25).
It is analogous for all biparametrical types of catalyzed reactions (Table 1).
Discussion
The analysis of data obtained shows that:
1) The values of the constants of biparametrical types of inhibition (Eqns. 1, 2, 5 – 7) and activation (Eqns. 9 – 11, 14, 15), are not subjected to additive dependencies on the values of the constants of monoparametrical types of inhibition (Eqns. 3, 4) and activation (Eqns. 12, 13) of the enzymes (Table 1);
They subjected to geometrical relationships (Pyphagorean theorem):
2) this opens an array of possibilities for calculation and correction of the values of Ki and Ka constants (Examples 1 – 4).
References
- Krupyanko VI. A vector method of representation of enzymic reactions. 3. Three-dimensional system of the K’m V’ I coordinates convenient for representation of enzyme inhibition and activation. Proc Biochem. 2004; 39: 825- 832. Ref.: https://goo.gl/dqMjBF
- Кrupyanko VI. Perspectives of Data Analysis of Enzyme Inhibition and Activation. Part 1: Use of the Three-Dimensional K’m V’ I Coordinate System for Data Analysis of Enzyme Inhibition and Activation. J Biochem Mol Toxicol. 2009; 23: 97-100. Ref.: https://goo.gl/BK2nqc
- Кrupyanko VI. Perspectives of Data Analysis of Enzyme Inhibition and Activation. Part 2: Parametrical Classification of Types of Enzymatic Reactions. J Biochem Mol Toxicol. 2009; 23: 101-107. Ref.: https://goo.gl/vRPeFp
- Кrupyanko VI. Perspectives of data analysis of enzyme inhibition and activation, Part 3: Equations for calculation of the initial rates of enzymatic reactions. J Biochem Mol Toxicol. 2009; 23: 108-118. Ref.: https://goo.gl/yyowYP
- Кrupyanko VI. Perspectives of Data Analysis of Enzyme Inhibition and Activation. Part 4: Equations for Calculation of Constants of Enzyme Activation and Inhibition. J Biochem Mol Toxicol. 2010; 24: 145-154. Ref.: https://goo.gl/F6m6Tf
- Krupyanko VI. Determination of intensity of enzyme inhibition and activation. Eur Chem Bull. 2014; 3: 582-586. Ref.: https://goo.gl/RxX2M2
- Krupyanko VI. Non-existence of secondary coordinates of intersects. Eur Chem Bull. 2014; 3: 815-822. Ref.: https://goo.gl/i8qkUU
- Krupyanko VI. Correction of Dixon Plots. Eur Chem Bull. 2015; 4: 142-153. Ref.: https://goo.gl/4bfDVP
- Krupyanko VI. Correction of Data Analysis Equations Relating to Two-Substrate Enzyme Catalyzed Reactions. Eur Chem Bull. 2016; 5: 354-363. Ref.: https://goo.gl/5P9gDz
- Webb L. Enzyme and metabolic inhibitors. Moscow: Mir Publishers. 1963; 6-862. Ref.: https://goo.gl/Ae4JrU
- Segel IH. Enzyme kinetics. J Wiley: New York. 1975; 3-957. Ref.: https://goo.gl/A54Kz6
- Dixon M, Webb EC. Enzymes. Moscow: Mir Publishers. 1982; 2: 3-481.








